Speed of the Fastest Human, Running
An educational, fair use website
| Bibliographic Entry | Result (w/surrounding text) |
Standardized Result |
|---|---|---|
| "World Records -- Men." Track and Field News, 2000. | "200 m… 19.32 s Michael Johnson (US) Atlanta, Ga…. 8/1/96" | 10.35 m/s |
| Moore, Kenny. Triumph and Tragedy in Los Angeles. Sports Illustrated. 31 July 1999. | "He had won the 100 in 9.99 on the first weekend of track and field." | 10.01 m/s |
| Fastest Man in the World Calculator. Runner's Web. | "Michael Johnson, 200 m, 19.32 s, 10.351966873706004 m/s, 37.267080745341616 km/h" | 10.35 m/s |
| "Running." Guinness Book of Records 1999. London: Random House, 1999. | "200 m: 19.32 Michael Johnson (US) Atlanta, Georgia, July 21, 1996" | 10.35 m/s |
As of June 2000, the fastest running human is Michael Johnson, the American track and field star who on August 1, 1996 set the world record of running 200 meters in 19.32 seconds. Johnson, by doing this, won an Olympic title in Atlanta, Georgia and broke the longest standing field record of the time; Pietro Mennea's 1979 record of 19.72 seconds. Johnson's record can be calculated to equal 10.35 m/s or 37.267 km/h. Johnson's events also include the 400 meter run which he ran in 43.18 seconds ranking him number one in the world in 1999. This broke the 11-year old record of American Butch Reynolds (43.29s). In this category, Johnson was undefeated throughout his career with forty four consecutive victories. An interesting fact to know is that in the animal kingdom Michael Johnson would be considered relatively slow; the cheetah, one of the world's fastest land animals, can sustain a top speed of about 30 m/s or 100 km/h -- three times the speed Michael Johnson can achieve.
Katarzyna Januszkiewicz -- 2000
| Bibliographic Entry | Result (w/surrounding text) |
Standardized Result |
|---|---|---|
| Mureika, Jonas R. "Fastest human running." email to the editor. 15 February 2001. | "The fastest recorded instantaneous velocity achieved by a human was supposedly by Donovan Bailey, who set the World Record in the 100 m (9.84 s). He was clocked at 12.1 m/s, although this figure is perhaps a bit rough (recorded by a radar gun). Accurate data was taken at the 1997 World Championships in Athens, where the top speeds of both Maurice Greene and Bailey were recorded at 11.87 m/s (althogh neither set records in the race -- Greene ran 9.86 s to Bailey's 9.91 s). Bailey was also clocked at 11.91 m/s in the 4 × 100 m relay final at the same championship." | 12.1 m/s (instantaneous, but unreliable) 11.91 m/s (instantaneous) |
| "I have run some simulations which suggest that Michael Johnson probably hit a maximum velocity of 11.6 m/s in his 19.32 s world record race, but was able to sustain speeds in excess of 10.0 m/s for the duration of the race (something no other 200 m runner has ever accomplished, in theory)." | 11.6 m/s (instantaneous) > 10.0 m/s (sustained) |
|
| Mureika, Jonas R. How Good Can We Get? Using mathematical models to predict the future of athletics. Athletics: Canada's National Track and Field/Running Magazine. (April/May 1998). | "Table 5: Predicted ultimate performances for men and women (from reference [1]). 100 m: Men 9.37 s, Women 10.15 s" |
10.672 m/s (average, projected) |
| Mureika, Jonas R. 10 m Splits for Various 100 m Final Events. University of Toronto | [see table below] | 11.80 m/s (instantaneous) |
The student who wrote the original essay focused her attention on the average speed of the record setting athletes. Average speed is found by dividing the distance covered by the total time elapsed. Readers of this essay might also find it interesting to know the instantaneous speed of the athletes; that is, the speed as measured over an vanishingly small time interval. Instantaneous speed is often thought of as the "actual speed" as it varies with the actions of the athlete. In contrast, the average speed is often viewed as an artifact of calculation -- one that summarizes a complex event with a single number.
In track and field, instantaneous speed can be approximated by fitting a smooth, continuous curve to a runner's split times -- the time for the runner to reach a set of equally spaced milestone distances. Split times for the 100 m dash are taken every 10 M. A table of split times with the calculated instantaneous speeds from the 1997 World Championships in Athens, Greece is shown to the right. Note that the first and second place runners had the same instantaneous speeds (11.80 m/s) at the 60 m split. A more detailed analysis of the data (see reference 1) indicated that they also reached the same maximum instantaneous speed of 11.87 m/s just before this point.
| Maurice Greene | Donovan Bailey | |||
|---|---|---|---|---|
| distance (m) |
time (s) |
speed (m/s) |
time (s) |
speed (m/s) |
| 000 | 0.00 | 00.00 | 00.00 | 00.00 |
| 010 | 1.71 | 08.71 | 01.78 | 08.90 |
| 020 | 2.75 | 10.47 | 02.81 | 10.55 |
| 030 | 3.67 | 11.14 | 03.72 | 11.28 |
| 040 | 4.55 | 11.50 | 04.59 | 11.63 |
| 050 | 5.42 | 11.67 | 05.44 | 11.76 |
| 060 | 6.27 | 11.80 | 06.29 | 11.80 |
| 070 | 7.12 | 11.68 | 07.14 | 11.70 |
| 080 | 7.98 | 11.57 | 08.00 | 11.55 |
| 090 | 8.85 | 11.51 | 08.87 | 11.38 |
| 100 | 9.73 | 11.30 | 09.77 | 11.00 |
An interesting and easy way to determine the instantaneous speed from the split times can be done using any basic data analysis program. Plot the distance against the split times and execute a curve fitting analysis. I chose to fit Maurice Greene's split times at Athens to a fourth order polynomial. The advantage of using this curve is that the software I have can determine the best fit coefficients in a fraction of a second.
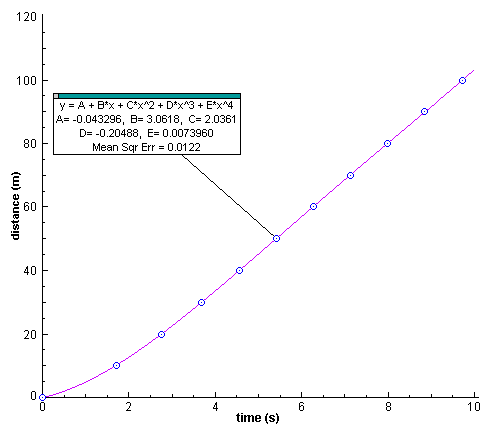
Instantaneous speed can then be found by taking the derivative of this graph (the slope of a line tangent to the curve at any point).

Which when graphed looks like this…

vmax = 11.78 m/s at t = 5.53 s
There is a serious problem with this graph, however, as it shows a non-zero initial speed. Sprinters are not allowed to "jump the gun"; that is, they must be at rest when the starter's pistol is fired. Such an event would surely have been detected by race officials and a false start would have been called. A proper model would have to reflect this fact.
The value of the derivative at the origin is zero for the second and higher order terms (so they get to stay), but the derivative of the first order term is a constant (so it has to be tossed). I chose to refit the split times to a polynomial with terms of order 2 through 6. It took about an hour for the analysis software to fit this curve to the data.
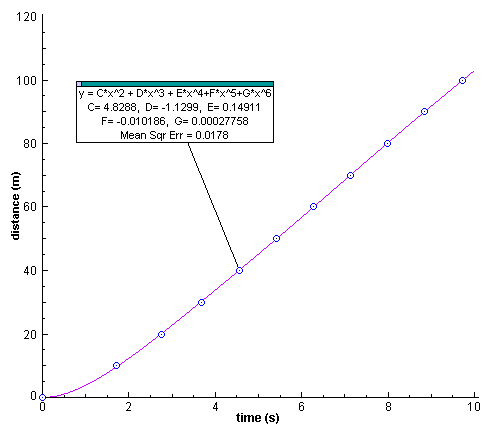
Again, instantaneous speed can be found from the derivative.
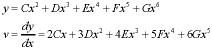
Which when graphed looks like this…

vmax = 11.80 m/s at t = 7.02 s
Is this curve better than the previous one? Well, yes. The initial velocity is now zero as one would expect.
Is this the perfect curve? Well, no. Check out the slope at the origin. You should recall that the slope of a speed-time graph is the acceleration. This curve shows a non-zero acceleration at the beginning of the race, which is against our expectations. The acceleration should build up quickly starting from zero. Again, the runners can't "jump the gun".
A workaround for this problem would be to drop the second order term from our polynomial and see what happens. Maybe I will try that someday, but given the sluggish response of the data analysis software I'm using, I doubt it. A new approach is probably necessary -- one that may not be appropriate for the level of this book.
Editor's Supplement -- 2001
| Bibliographic Entry | Result (w/surrounding text) |
Standardized Result |
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| International Association of Athletics Federations, 100 Meters Records, 20 August 2008. |
|
10.32 m/s (average) |
||||||||||||||
| International Association of Athletics Federations, 200 Meters Records, 20 August 2008. |
|
10.36 m/s (average) |
||||||||||||||
| International Association of Athletics Federations, 100 Meters Records, 20 August 2009. |
|
10.44 m/s (average) |
Records were meant to be broken. We now have a new fastest human and his name is Usain Bolt.
Editor's Supplement -- 2008, 2009
External links to this page:
- Speed Records, Racers, Machines, Ways, Reading, Speed101
- Horse versus human, who would win? Jason Kottke