2. Strange & Complex
2.3 Mandelbrot Sets
Julia sets rendered with Julia's Dream. Mandelbrot sets rendered with MandelZot and Object Mandelbrot. Movies rendered with MandelMovie.
The factor that determines whether a Julia set is wholly connected or wholly disconnected is the parameter value c. Thus it would be instructive to plot the behavior of the Julia sets for all parameter values. The resulting construction would be the complex analog of a bifurcation drawing. At first glance, this seems a daunting task. Plotting every possible Julia set and then examining it to determine whether it was connected or not would take an eternity. Luckily for us, however, we need only study the behavior of one point in the complex plane. Given a family of complex iterative maps, the set of all parameter values that produce wholly connected Julia sets is determined by the behavior of a single seed value: the origin. If the orbit of the origin never escapes to infinity then it is either a part of the set or it is trapped inside it. If the origin is a part of the set, the set is dendritic. If it is trapped inside the set, the set is topologically equivalent to a circle and thus is wholly connected. This trick was discovered by the Polish-American mathematician Benoit Mandelbrot and in his honor the set of all parameter values whose Julia sets are wholly connected is called a Mandelbrot set. The Mandelbrot set for the quadratic mapping
ƒ: z → z2 + c
is shown below for all parameters
c = x + iy
in the range
x = [−2, ½] y = [−2, 2].
Some wholly connected Julia sets were also added and their approximate location in parameter space indicated. This type of arrangement is known as a constellation diagram.
 |
Note the similarities between any Julia set and the corresponding parameter space region on the Mandelbrot set. The Julia sets that are pinched vertically are found where the Mandelbrot set is pinched vertically. Likewise the set which is pinched horizontally is found on the extreme right side in a region that is pinched horizontally. The dendrite corresponds to a parameter point on a filament at the top and the long tail to the left produces a Julia set that is similarly long and tail-like. Such similarities are found at the microscopic level as well. Not only does the Mandelbrot set tell whether a corresponding Julia set is connected or disconnected, it also suggests its appearance.
An interesting way to see the variety of Julia sets is by means of a cascade.
- Describe a "connect-the-dots" path through the Mandelbrot set
- Draw the corresponding Julia set at each point
- Assemble the sets into a movie and play it
 cascade as the banner graphic from 1999–2016. |
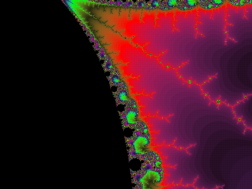
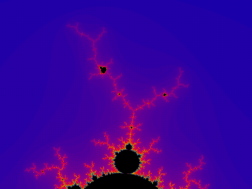
The two cascades below below use a coloring technique common to fractal images. Points inside are colored black while those outside are assigned a particular color that indicates how quickly the point escapes to infinity. This technique accentuates some of the details that might otherwise be hidden.
 |
 |
The main body of the Mandelbrot set is a cardioid with a series of successively smaller circles attached to it in a chain running along the x-axis in the negative direction. The attachment points on this chain correspond to the bifurcation points of the simple one-dimensional iterative map. Thus, each circle on the x-axis corresponds to a region of differing periodicity. The ratio of the diameters of successive circles approaches Feigenbaum's constant δ [delta]. Note too, how the long tail-like region is punctuated with little islands. This corresponds to the chaotic regime and the islands to the odd period windows. Recall how in the one-dimensional case the structure of the windows was similar to the overall bifurcation diagram. Likewise these windows are miniature mutated copies of the whole Mandelbrot set. This structure also repeats itself radially around the set. Each major bulb has smaller bulbs budding off it which in turn have bulbs attached to them and so on. The whole set is bristling with filaments, each with its own array of window-like, mutated copies of the whole set. The Mandelbrot set is a wholly connected archipelago of self-similar islets linked by an array of extremely twisty, ever branching fibers. There is no end to the detail present in the Mandelbrot set as the following set of successive magnifications show.
The diagrams below give some idea of the variety of structures that can be found in the Mandelbrot set. The first row of diagrams show some of the decorations attached to the bulbs surrounding the bays. Note how the branching patterns are similar to each other, yet still unique. (Incidentally, the number of branches equals the period of the points within a particular bulb.) The second row of diagrams show some of the "mini-mandelbrots" that crop up along the filaments. Each is unique, but yet still unmistakably a Mandelbrot set in appearance. These pictures illustrate an important characteristic of the Mandelbrot set. Whereas fragments of a Julia set are strictly similar to the set as a whole, fragments of the Mandelbrot are only quasi-similar to the set as a whole. Furthermore, the motif of this quasi-self-similarity varies from one region to another and from one level of magnification to another.
One way to picture Mandelbrot and Julia sets is as complex ordered pairs (c, z) such that the mapping
ƒ: z → z2 + c
does not escape to infinity when iterated. Julia sets are slices parallel to the z-axis while the Mandelbrot set is a slice along the c-axis through the origin. As the coordinate system is complex, however, these "axes" are actually planes. The Mandelbrot and Julia sets are therefore two-dimensional cross sections through a four-dimensional parent set; the mother of all iterated quadratic mappings so to speak.
The exotic sets shown in the following movie are successive slices through the four-dimensional mother set as we shift the cross sectional plane from the z = 0 plane of the Mandelbrot set to the c = −1 plane of a particular Julia set (the San Marco Dragon).
 |
In this chapter, I have touched on some of the topics arising out of the study of iterated mappings, expanding the simple one-dimensional case to the multi-dimensional and complex realms. By extension, one can imagine other related systems worthy of an equal amount of study. We have not addressed the analysis of other iterated mappings on the complex plane: higher powers such as
z4 + c or z6 + c
trigonometric functions like
cos z + c
hyperbolic or exponential functions, and so on. We also have not dealt with functions driven by periodic or random fluctuations, nor those with discontinuities and corners. And if we allow complex numbers, we must also allow quaternions, octernions and the rest of their higher dimensional cousins. Not surprisingly, someone has already done most of this.